こんにちは、阿比留です。
某日。いつものようになぞなぞに勤しむKくんとRくん。
(2人は自他ともに認めるなぞなぞガチ勢🔥🔥🔥)
脳トレの第2問を考えています。
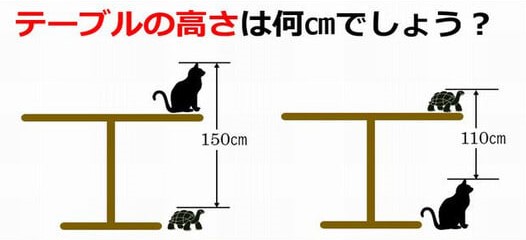
すでに連立方程式を習っている中2のKくんは、
テーブルの高さを xcm、ねこの身長をacm、かめの身長をbcmとして、
連立方程式を作ってこの問題を解いていました。
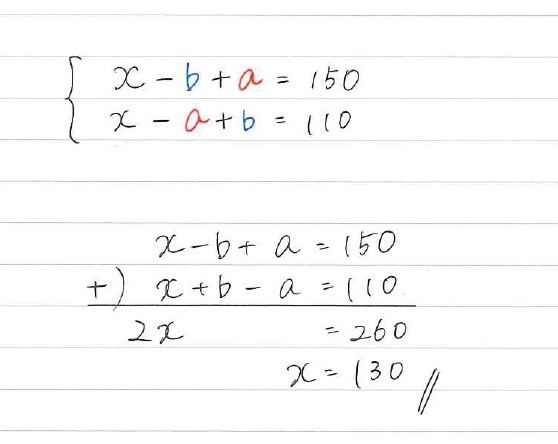
それぞれの図から式を2つ作って、
2つの式を足すと(加減法)、
ちょうどaとbが消え、x だけの式になります。
計算から、テーブルの高さは130cmということが分かりました。
実はこの問題、連立方程式を使わなくても、
小学校で習う知識だけで解けるようになっているんです。
模範解答はこちら。
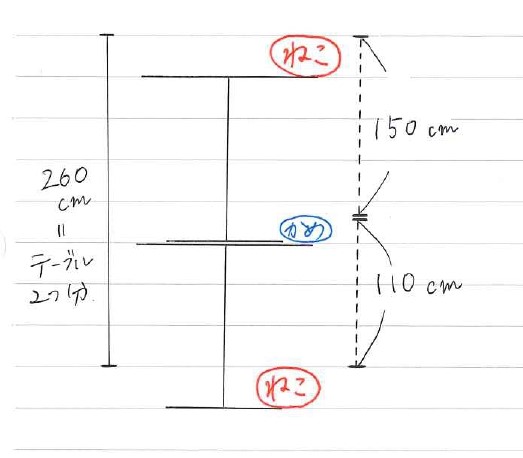
この図を縦に並べると、
下のねこの上部から、上のねこの上部までが260cmとなり、
これはちょうどテーブル2つ分の高さになりますので、
テーブル1つの高さは130cm と分かります。
Kくんのやり方と模範解答、
実はもとになる考え方は同じなのです。
連立方程式の「加減法」というのは、
2つの式の共通部分を抜き出すことで、
残りの部分から解を求めるやり方です。
模範解答では、図を縦に並べることで、
ねことかめの高さが消え、
テーブル2つ分の高さだけが残るので、
答えを求めることができました。
数学の応用問題は、
センスでしょ!とか、ひらめかないから解けない…という声を聞きます。
最初は公式丸暗記でも、解法丸暗記でも大丈夫。
というか、それを繰り返すことで体に染み込んでいくものだと思います。
そうして、何度も何度も繰り返して、
「やり方は覚えた!解けるようになった!」という子は、
なぜそうなるのかを考えてみると、一歩先のレベルに進めるかもしれません。
(教科書には、公式の仕組みまで書いてあります!)
そして、一見暇つぶしのようにも見えるなぞなぞ・脳トレにも、
勉強につながる深~い意味が含まれていることを知ってもらえたら嬉しいです🙌












