今回は「学問案内」から少し離れ、日々の勉強がちょっと楽しくなるお話をお届けします。
みなさん、美術における「黄金比」という言葉を聞いたことがあるでしょうか?
たとえば、
レオナルド・ダ・ヴィンチ 作『モナ・リザ』
葛飾北斎 作 『冨嶽三十六景 神奈川沖浪裏』
これらの作品はとても美しい構図であるとして有名です。
また、パルテノン神殿をはじめ、建築分野にも多く利用されています。
現代でもアートデザインの世界では欠かせない「美の法則」
その美しさの秘訣が「黄金比」というものです。
▼ 葛飾北斎 『冨嶽三十六景 神奈川沖浪裏』
海外の画家にもインスピレーションを与えたとして有名です。
波の形や全体の構図に黄金比が使われています。
引用:東京富士美術館
実は、この「黄金比」というのは数学と深いつながりがあります。
今回は「黄金比」についてご紹介します。
黄金比の紹介
・そもそも黄金比ってなに?
・どうして 1 : (1+√5) / 2 になるの?
・1 : (1+√5) / 2 ってだいたいどれくらい?
・そもそも黄金比ってなに?
黄金比とは特殊な線分比としてあらわすことができます。
ある線分をa:bに内分 (=内側に点を打って分割) し、a : b = b : (a+b) となるのが「黄金比」です。
▼ 黄金比の線分。外中比とも呼ばれるそうです。
※ちょうどいい画像素材がないためマウス作図でお届けします。
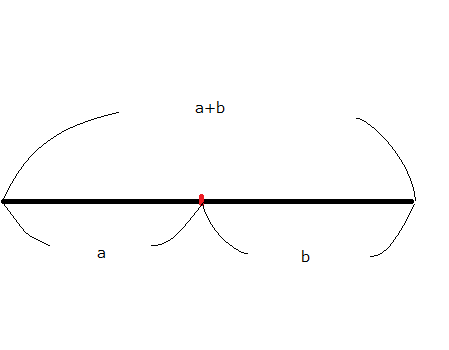
これを満たすのが 1 : (1+√5) / 2 と言われています。
・どうして 1 : (1+√5) / 2 になるの?
さて、比例式の性質を覚えていますか?
例えば
3 : 2 = 9 : x
という式が出てきたとき、
3x=2×9
という風に 外側×外側=内側×内側 という式が成り立ちます。
これを解くと
3x=2×9
x=18 となりますね。
同じように、先ほどの黄金比を比例式で表してみます。
a : b = b : (a+b)
これを先ほどと同様に 外側×外側=内側×内側 で表し、整理していきます。
a(a+b)=b2
a2+ab=b2
a2+ab-b2=0
ここで仮にa=1としてbの値を求めてみましょう。
12 +b-b2=0
この式を並びかえると
-b2+b+1=0
b2についている負の記号(係数:-1)が邪魔なので、全体に-1をかけます。
すると
b2-b-1=0
ここで役に立つのが中学校3年生で習う2次方程式の「解の公式」です。
解の公式に当てはめることで、bの値が求められます。
▼ 2次方程式の解の公式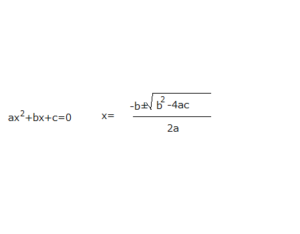
b2-b-1=0 を解の公式に当てはめやすいよう、 x2-x-1=0 とすると…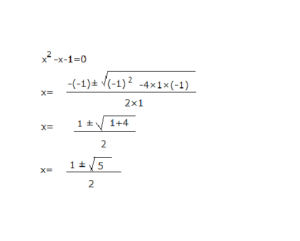
線分において 答えが負の数になってしまってはおかしいですよね?
(線の長さの話ですから必ず正の数になるはずです)
そのため、正の数だけを採用します。
a : b の比を 1 : x としたとき、x= (1+√5) / 2 となるわけです。
1 : (1+√5) / 2 が黄金比となることがこうして説明できましたね。
・1 : (1+√5) / 2 ってだいたいどれくらい?
(1+√5) / 2 と言われても、具体的にどれくらいの値なのかピンときませんよね??
そこで使えるのが「近似値」という考えです。
√5=2.236079…
語呂合わせで『富士 山麓(ふじ さんろく)オウム 鳴く』と紹介されることが多いです。
ここでは小数第2位を四捨五入し、
√5=2.2 とします。
すると、
(1+√5) / 2 = (1+2.2) / 2
=(3.2) /2
これは3.2÷2 ということですので、 (1+√5) / 2 =1.6となります。
つまり、
黄金比である 1 : (1+√5) / 2 というのは、およそ 1 : 1.6 ということですね。
▼ レオナルド・ダヴィンチ 『モナ・リザ』
顔の幅について横 : 縦 が 1 : (1+√5) / 2 の黄金比になっているそうです。
私たちが毎日の生活で目にするもののあちこちに、この黄金比は隠れています。
「素敵だな」と思うデザインや作品、
「よく見かけるなあ」というロゴやマーク。
少し観察してみてください。
もしかしたらそこにも黄金比が隠れているかもしれませんよ!
今後もブログ・Twitterで情報発信していきますので
Twitterのフォローも是非よろしくおねがいします🐾
↓寿都町公設民営塾 Twitter
- 投稿タグ
- 学問トピック